4D成像雷达中的距离徙动及补偿方法分析

 

在4D成像雷达的信号处理过程中，为提高回波信号的信噪比（SNR），增加雷达的探测感知能力，采用脉冲积累的方式来做2DFFT，SNR的增量与脉冲积累数相关。但当脉冲积累的时间过长，或者目标运动速度过快，回波信号在脉冲积累时，会发生跨距离单元现象，产生距离徙动，分散目标能量，影响雷达检测性能。

为讨论距离徙动影响和对应补偿方法，建立以下仿真模型。在一个距离分辨率为，脉冲调制周期为的系统中，假设第一个距离单元对应的距离为，目标距离，对应的距离单元个数为。目标以径向速度靠近雷达，回波信号中目标在第个脉冲上的距离表示为：

                     (1)

此时，目标对应的距离门为，时间延迟为

                            (2)

发射雷达信号

                           (3)

则第个脉冲的回波信号

     (4)

上式进行下变频后，得到基带信号

(5)

上式通过匹配滤波器，设 通过匹配滤波器后的波形为 ，B为的带宽。则通过匹配滤波器后波形为

 (6)

上式为连续信号，进行离散化后信号可得到第个脉冲的快时间采样向量为

 (7)

得到快-慢时间矩阵

 (8)

距离徙动后频谱如下：

发生距离徙动的原因是在一个CPI内，目标跨越了多个距离门。目标在第个脉冲相对于0脉冲运动距离为。对第个脉冲，目标在快时间上平移个距离单元即可在的离散时间傅里叶变换（DTFT）为 。根据DTFT的时移性质，可由下面方式实现距离平移补偿

               (9)

其过程如下图所示。

以某一速度进行补偿，其结果如下图。可以看到，目标1进行补偿后，距离不再徙动，进行MTD后信号增强。

                                          

 

   上面只是利用了傅里叶变换的时移性质，将快时间维的距离补偿变换至频域进行操作，并未给出快时间向量频域的数学形式，现对其说明。

    在没有发生距离徙动的理想情况下，假设目标在1个CPI内没有位移，但是有速度，这种假设条件下，1个CPI内所有脉冲的快时间向量通过匹配滤波器后都为 。根据傅里叶变换的时移性质

                     (10)

可知的傅里叶变换为

                (11)

理想情况下，慢时间维的多普勒频率的复正弦波以慢时间 为采样时间间隔进行采样。因此，慢时间维信号可以表示为

           (12)

上文所述中，忽略距离徙动的快时间-慢时间矩阵为

  (13)

对上式进行FFT得到

 (14)

考虑实际距离徙动，对(6)进行FFT，得到

(15)

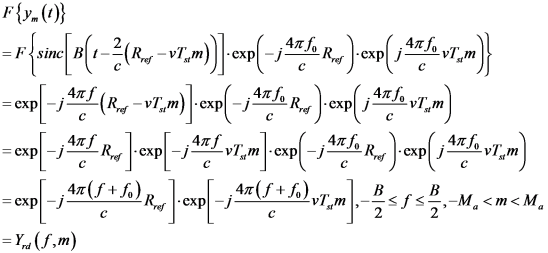
比较(14)和(15)可以看出，理想情况下和没有交叉项，发射距离徙动时存在和的交叉项。当时，慢时间的相比变化率比理想情况下大；当时，慢时间的相位变化率比理想情况下小；当时，式(14)和式(15)一致。校准距离徙动即找到方法消除和的交叉项。

    一种方法是，在(15)后乘（）消除和的交叉项，这实际上就是上面通过距离平移补偿的方法，这种方法必须准确知道目标的速度，并且只能校正一个目标的距离徙动。

    另一种方法是通过慢时间坐标变换来进行距离徙动的校正，也就是keystone方法。考察(15)式的慢时间项，它在时刻，对复正弦信号的采样，将慢时间项写成连续时间的函数，即

       (16)

定义

                            (17)

则

   (18)

可以看到，式(18)通过坐标尺度变化，消除了和的交叉项，变为理想的情况。此时只需要对快时间维进行逆FFT变换，对慢时间维进行傅里叶变换，即可以得到“聚焦”的距离-多普勒图像。

常见的keystone实现方法有sinc插值法、DFT-IFFT算法和CZT算法三种。

1)                      Sinc插值算法

   坐标转换前后如下图所示。变换前的数据点如绿色实心点所示，在快时间频率-慢时间域上呈现矩形形式排列。此时对于任意的快时间频率，对应的慢时间采样间隔（等效脉冲重复间隔）都是一样的。keystone变换本质上对原格式数据根据快时间频率进行插值处理，插值后的数据点如红色空心圆所示。

可以看到， 时，进行了坐标拉伸操作，越大，慢时间采样间隔越大；时，采样点位置没有发生变化；时，进行了坐标压缩操作，越小慢时间采样间隔越小。插值后的数据点形成一个倒梯形的形状，这也是“keystone”名称的由来。插值完成后，需要再将插值的数据点重新排列成之前的矩形形式，此时Keystone变换完成。

sinc插值法利用率采样定理的思想。该方法将已有的信号按照快时间相同频率进行分组，分别对每组进行处理，将其作为连续信号的采样样本值，通过使用低通滤波器对该信号滤波得到连续信号，再对该连续信号所需要的点进行再次采样实现插值。理想低通滤波器在频域上是一个矩形窗，对应时域为Sinc函数。频域相乘等于时域卷积，为了在时域上重建信号，需要把采样后的信号与Sinc函数进行卷积计算。

    离散卷积的表达式为

               (19)

则Sinc插值法可以表示为

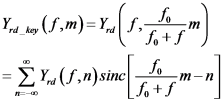
                    (20)

经过keystone变换后，1个CPI内慢时间脉冲数取值范围变为

                        (21)

当时，取值范围大于；当时，的取值范围小于。在实际应用时，一般限制keystone校正后的脉冲数仍为。

2)                      DFT_IFFT算法

DFT-IFFT算法是根据傅里叶尺度变换的性质得到的,首先回顾傅里叶变换的尺度变换性质。

                     (22)

为了从得到，可以先对的慢时间维进行傅里叶变换得到，如果可以得到，则对k进行逆傅里叶变换即可得到

          (23)

DFT的表达式

                (24)

第一次傅里叶变换采用变换尺度的DFT变换直接得到，即

                  (25)

然后再对的k做逆傅里叶变换

                 (26)

    需要注意的是，FFT算法是利用了的周期性和对称性才能实现，而第一次DFT的傅里叶变换基是变尺度的，因此不能使用FFT实现。第二次的逆傅里叶变换可以使用FFT快速算法。因此这种实现方法称为DFT-FFT算法。如果发生速度模糊，则需要补偿。

3)                      CZT算法

DFT-IFFT算法中指出，由于存在尺度上的不同，第一次只能采用DFT进行运算，大大增加了运算量。根据上面分析，当求keystone变换后慢时间对应的多普勒域时，尽管存在尺度上的不同，若仍以未变换前的慢时间对应的多普勒域表示频谱采样点的位置时，K个采样点在单位圆上的分布间隔变为

                              (27)

它是关于的函数，不再是在整个圆周上均匀分布，这也是不能应用FFT进行计算的原因。Chirp-Z变换（CZT）是求上述非等间隔情况下各点采样值的快速算法，其基本原理是采用螺线抽样，求各采样点有限长序列的z变换为

                      (28)

为了使得可以沿着z平面更一般的路径取值，故沿z平面上的一段螺线作等分角的采样，记采样点为

                     (29)

其中，M为所要分析的复频谱点数，不一定等于N；

                                (30)

为起始抽样点的矢量半径长度；

为起始抽样点的相角；

为螺线的伸展率，表示半径为的一段圆弧。若又有，则这段圆弧是单位圆的一部分；

为两相邻抽样点之间的角度差。

当M=N，,时，各采样点均匀等间隔地分布在单位圆上，就是序列DFT。此时，如果取，为任意值，则所求的DFT是一段任意频率范围的频谱，也就是单位圆上某一段的频谱。这与直接计算DFT求整个频率范围的频谱是不一样的，即使调整N的大小，例如增加N，也只能增加一段频率范围的计算量而已。

    将带入变换的表达式中，得

             (31)

其中

               (32)

将线性卷积用循环卷积进行计算，从而可以变换到频域用FFT进行快速运算。下面给出CZT的实现流程图。

使用CZT进行keystone变换，只需令

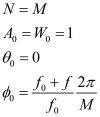
                            (33)

即，，然后按照CZT的计算歩奏进行计算。

在一个CPI内，雷达与目标之间的距离一直在变化，该变化对应雷达接收的回波信号产生时延差。如果距离变化超过一个距离分辨单元，就会导致距离徙动。距离徙动会导致4D成像雷达目标回波信号能量分散，信噪比降低，影响成像质量。可通过距离徙动校正算法，将距离徙动曲线校正为平行于方位向的直线，其斜距的变化小于距离分辨单元的一半，满足在一个CPI内，目标距离变化不超过一个距离分辨单元。